ESPEJOS CONCAVOS
En el estudio de estos espejos seguiremos la misma marcha que en el de
los espejos planos, empezando
por determinar experimentalmente la naturaleza, posición y magnitud de
sus imágenes.
La
abertura del espejo o su diámetro AB
del circulo base; su abertura angular es el ángulo ACB
Nos limitaremos en nuestro estudio a los espejos de pequeña abertura, con
diámetro inferior a la mitad del radio de la esfera, que corresponde a un
ángulo menor que 20 a 25º.
1.
Tomemos un objeto muy
luminoso situado a gran distancia del espejo;
suele decirse
en este
caso que
el objeto
está infinitamente alejado del espejo o que está situado en el
infinito (para ello basta que
el objeto esté situado a una distancia comprendida entre
50 a
100 veces el
radio de curvatura del
espejo). Podrá utilizarse
para ello una lámpara eléctrica. Tratemos
de recoger los rayos reflejados sobre una pequeña pantalla de cartón
blanco, y comprobemos que la mitad la distancia entre el centro de espejo
y su vértice se tiene una imagen muy clara, pero muy pequeña, e invertida,
de la lámpara y de los objetos situados a su alrededor;
el máximo de nitidez se
obtiene cuando
la pantalla
está situada
perpendicularmente al
eje óptico que pasa por la lámpara. Este plano en el que se encuentran
las imágenes de todos los puntos infinitamente alejados,
se denomina plano focal del espejo.
2.
Aproximemos el
objeto al
espejo, de
forma que
la imagen permanezca
al principio en el plano focal, después, a medida que el objeto se
aproxima al objeto.
3.
La imagen de la pantalla es siempre invertida, y aumentada cada vez
más. (fig. 13).
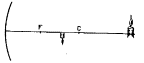 Figura
13
Figura
13
El
ramillete mágico (El espejo da una imagen real
3.
Cuando el objeto llega al plano frontal (perpendicular al eje óptico)
que pasa por el centro C del espejo, la pantalla donde recoge la imagen debe estar también
colocada en el mismo plano; esta imagen,
siempre invertida (fig. 14), tiene exactamente la misma dimensión que el
objeto.
|
|
Fig.
14
4.
Si continúa aproximándose el objeto, la imagen sigue alejándose
cada vez más rápidamente, llegando
a ser, siempre invertida,
mayor que el objeto.
5.
Cuando el objeto se encuentra en el plano focal, la imagen se
encuentra en
el infinito
su dimensión
es enorme
y, por consiguiente,
es muy poco luminosa. Encontramos
en los párrafos 4 y
5 resultados conformes con el
principio del retorno
inverso de la luz relativo a la intercambialidad de la imagen y el objeto.
6.
Cuando el objeto sobrepasa el plano focal,
aproximándose al espejo, no es posible recoger la imagen en una
pantalla; la imagen, que hasta ese momento era real, se hace virtual.
Si nos colocamos de forma que recibamos en el ojo una parte de los
rayos reflejados, observamos
una imagen todavía mayor que el objeto,
pero del mismo sentido, es
decir, derecha,
y que disminuye cuando el objeto se aproxima al espejo (fig. 16)
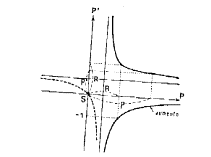
Fig.
16
El
espejo cóncavo puede dar, pues, imágenes reales y virtuales. Las imágenes
y el objeto se desplazan siempre en sentido inverso.
Es posible,
valiéndose de los resultados
de las
experiencias precedentes, trazar una curva que permita encontrar la
posición de la imagen, conocida la del objeto, o inversamente.
Tomemos dos es de coordenadas rectangulares SP
y SP' (fig. 16).
Sobre el eje abscisas SP se llevan las distancias p
del objeto al vértice del objeto, y
sobre el
eje de ordenadas SP'
las distancias
correspondientes p' de la
imagen del espejo. La curva
que une los representativos obtenidos pasa por el punto de coordenadas
p = R y p’ = R la
curva es una hiperbóla equilátera,
cuyas asintotas son paralelas a
los ejes de coordenadas, a la distancia
R
denomina distancia
o longitud focal f
la
mitad del radio de altura R del
espejo.
También
se puede representar por una curva el aumento lineal, es decir, la relación
entre las dimensiones de la imagen y el objeto a las diversas distancias p del objeto al espejo. Para
ello a con medir la imagen en la pantalla.
Esta relación será negativa cuando la imagen sea invertida, como
sucede cuando p varia entre f
y el infinito, forma se obtiene una rama de otra hipérbola.
DE
LOS ESPEJOS CONCAVOS
Aplicando
las leyes
de la
reflexión a
los espejos
esféricos cóncavos es posible obtener la dirección de los rayos
reflejados, debiendo llegarse
de nuevo,
mediante razonamiento,
a los resultados de
las experiencias anteriores, la teoría permitirá establecer, además, fórmulas matemáticas
y construcciones gráficas que fijen la posición, la dimensión y el
sentido de la imagen.
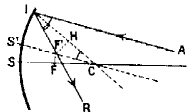
Sea
M un espejo esférico (fig. 17)
|
|
Fig.
17
de
centro C y vértice S,
y consideremos un rayo incidente Al
procedente del objeto A,
situado cerca del eje óptico,
y que encuentra el espejo en I.
Para determinar el ángulo de incidencia que traza la normal a la
superficie en el punto I; como en una esfera los radios son perpendiculares a los planos
tangentes, estos radios son:, por consiguiente, las normales buscadas.
El rayo reflejado IR tendrá, pues, que: 1)
Estar en el plano AIC, que
tomaremos como palmo de la figura, y
2) Formar con IC un ángulo
igual al AIC.
Para encontrar más fácilmente la dirección del rayo
reflejado, se traza por el centro C
un radio CS' paralelo al
rayo luminoso incidente Al
(CS’ es un eje óptico secundario).
El rayo reflejado IR
corta CS'. En efecto, los ángulos
AlC y ICS' son iguales por
alternos internos, y el triángulo ICF'
es asósceles, siendo FC = IF’.
Si se traza
desde F'
la perpendicular F'H
a IC
se tendrá:
IH
= HC R siendo
R el radio de la esfera; en
el triángulo IF’C,, F'C difiere
muy poco de C, y,
por lo tanto, de R
y F’ está muy
cerca del punto medio de S’C.
En el triángulo HCF’ HC = F’C cos
2
ICF’,
por lo que, si î es el ángulo
de incidencia:
HC =
R
= F'C cos î
2
FC = R
2 cos
En
virtud de la hipótesis que hemos formado, la abertura del espejo la
semiabertura angular es pequeña, y el ángulo î
= ICS' es inferior a la
semiabierta angular, y por consiguiente menor de 10%;
es decir, cos î está
comprendida entre Cos 0º y
Cos. 10º, o sea entre 1 y 0,985.
F'C, que es igual a R
, cuando î es muy pequeño
y próximo de 0º
2
aumenta
ligeramente hasta R, cuando
î vale 10º, que es ya un ángulo notable.
2