Intensidad del Campo Magnético

Si lanzamos diversas partículas cargadas a un campo magnético, este ejercerá sobre ellas cierta fuerza magnética. Esta fuerza magnética es perpendicular al plano que forman los vectores velocidad y campo magnético. De esto, podremos comprobar que la fuerza magnética sobre una partícula es proporcional a su carga, a su velocidad, y al seno del ángulo que forma el vector campo magnético con la velocidad de la partícula, es decir que mientras más rápido se mueva una partícula cargada, mayor será la fuerza magnética ejercida sobre ella.

 Todos estos efectos se han podido comprobar con tubos de rayos catódicos, parecidos a los que se usan en los televisores. En estos tubos, que son hechos al vacío, los electrones son producidos mediante el efecto termoiónico en un filamento caliente (cátodo) y aceleradas hacia una placa (ánodo) a potencial eléctrico más elevado; los electrones pueden atravesar esta placa porque es hueca en el medio. Pasado el ánodo, los electrones ya acelerados golpean a gran velocidad contra una pantalla fluorescente, donde producen una mancha en el punto de incidencia.

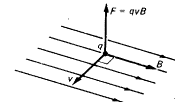En la figura vemos un tubo de rayos catódicos

 

La figura nos muestra los vectores involucrados en el campo magnético.

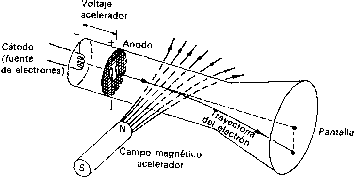
 Si acercamos un imán al tubo, observamos una desviación de la mancha luminosa en la pantalla. Esta desviación va a depender de la orientación del imán respecto a la trayectoria inicial de los electrones, y también a la intensidad del campo. Variando la distancia del imán al tubo, de modo que varíe la intensidad del campo magnético, y modificando el voltaje aplicado entre el cátodo y el ánodo, de modo que varíe la velocidad de la carga, se puede analizar como afectan estos dos factores a la fuerza que actúa sobre la carga.

Luego, se designa como B la intensidad del campo magnético, y vemos que si lanzamos una partícula en dirección perpendicular a un campo magnético, podemos establecer la relación entre las magnitudes F, v y B:

F = qvBsena

Newton = Coulomb X m/s X tesla 

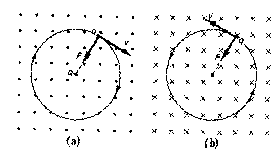Ahora, cuando un campo magnético es perpendicular al plano del papel y está dirigido hacia fuera, se representa por puntos (figura a) y cuando está dirigido hacia dentro se representa por cruces (figura b). 

La relación anterior nos permite determinar el campo magnético si conocemos la fuerza, la velocidad y la carga. La unidad de medida del campo magnético en el SI es el Tesla (T). Deducimos entonces de las unidades de las otras magnitudes que la intensidad de un campo magnético va a ser de 1 Tesla si una carga de 1 Coulomb que se mueve perpendicularmente al campo magnético con una velocidad de 1 m/s experimenta una fuerza de 1 Newton. Ahora, si aislamos el valor B de la ecuación, nos queda: 

B=  ____F_____

       qvsena

Esta expresión se reduce si el ángulo es de 90 grados, y no se puede definir si el ángulo es de 0 grados.

Otra unidad empleada algunas veces para medir el campo magnético es el gauss. Su relación con el tesla es 1 tesla = 10 gauss